Phương trình (Hằng đẳng thức) bao gồm 7 phương trình cơ bản nhất mà người học toán nào cũng cần nắm vững. Vì vậy, có hằng số phương trình không tí nào? Hãy tham khảo bài viết này của ku89.
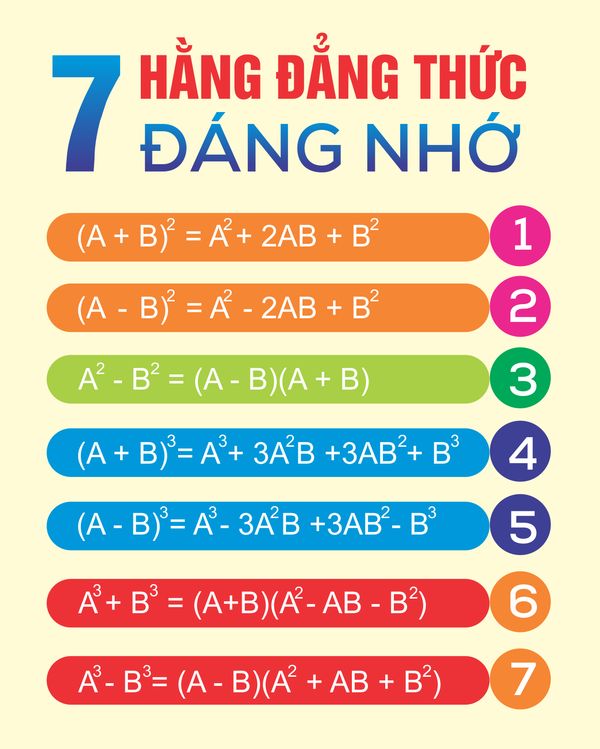
7 Hằng số Bình đẳng Khó quên (hằng đẳng thức)
Tổng bình phương
một bên: (a + b) 2 = a2 + 2 * a * b + b2
giải thích: Bình phương của tổng bằng bình phương của số thứ nhất cộng hai lần tích của số thứ nhất và số thứ hai, cộng với bình phương của số thứ hai.
bình phương chênh lệch
bình đẳng: (a – b) 2 = a2 – 2 * a * b + b2
giải thích: Bình phương của một hiệu bằng bình phương của số thứ nhất trừ hai lần tích của số thứ nhất và số thứ hai, cộng với bình phương của số thứ hai.
sự khác biệt giữa hai hình vuông
bình đẳng: a2 – b2 = (a – b) * (a + b)
giải thích: Hiệu giữa hai bình phương bằng hiệu giữa số thứ nhất và số thứ hai nhân với tổng của số thứ nhất và số thứ hai.
tổng các hình khối
bình đẳng: (a + b) 3 = a3 + 3 * a2 * b + 3 * a * b2 + b3
giải thích: Lập phương của tổng bằng lập phương của số thứ nhất, cộng ba lần tích bình phương của số thứ nhất với tích của số thứ hai và thêm tích ba lần của số thứ nhất với bình phương của số thứ hai. số. Thêm, thêm khối lập phương của số thứ hai.
Đây là một dạng của hằng đẳng thức bậc ba. Soạn bài Đêm nay Bác không ngủ chi tiết
khối lập phương khác nhau
bình đẳng: (a – b) 3 = a3 – 3 * a2 * b + 3 * a * b2 – b3
giải thích: Lập phương của hiệu bằng lập phương của số thứ nhất trừ ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng ba lần tích bình phương của số thứ nhất nhân với bình phương của số thứ hai, sau đó trừ lập phương của số thứ hai.
tổng của hai khối
bình đẳng: a3 + b3 = (a + b) * (a2 – a * b + b2)
giải thích: Tổng của hai lập phương bằng tổng của số thứ nhất và số thứ hai nhân với bình phương bị thiếu của hiệu.
Sự khác biệt giữa hai hình khối
bình đẳng: a3 – b3 = (a – b) * (a2 + a * b + b2)
giải thích: Hiệu của hai lập phương bằng hiệu của số thứ nhất và số thứ hai nhân với bình phương còn thiếu của tổng.
Làm thế nào để ghi nhớ một cách hiệu quả bảy phương trình khó quên
Dưới đây là 3 cách nhớ 7 hằng đẳng thức khó quên lớp 9 hiệu quả nhất mà ku89 đã đưa ra cho các bạn:
luyện tập thường xuyên
Học bằng cách làm. Thực hành thường xuyên sẽ giúp bạn ghi nhớ và sử dụng bảy hằng đẳng thức (hằng đẳng thức) thành thạo hơn.
Bạn có thể thiết kế bài tập dưới nhiều dạng như điền vào chỗ chấm, cho một phần, viết ra một phần khác.
viết trong notepad
Bạn có thể viết 7 hằng đẳng thức giống như cách học từ vựng tiếng Anh vào những tờ giấy nhớ nhỏ màu và dán lên góc học tập.
Bài học rút ra qua bài hát
Những từ tương đương có thể khó nhớ khi đọc to, nhưng việc đưa chúng vào một bài hát sẽ giúp bạn dễ dàng hơn.
Hiện tại đang có bài “Rốt cuộc” về 7 hằng đẳng thức. Giai điệu hay này đã thu hút sự quan tâm của rất nhiều bạn trẻ.
Nhờ đó, việc ghi nhớ bảy hằng số bằng nhau không còn nhàm chán mà còn thuận tiện hơn.

Bài tập về 7 hằng đẳng thức đáng nhớ
Để củng cố 7 hằng đẳng thức đáng nhớ (hằng đẳng thức), chúng ta cùng giải bài tập SGK toán.
Giải câu hỏi Trang 9 SGK Toán 8 Tập 1
a và b là hai số bất kỳ, hãy tính (a + b) * (a + b).
Hướng dẫn giải pháp
(a + b) * (a + b) = a * (a + b) + b * (a + b)
= a2 + a * b + b * a + b2
= a2 + 2 * a * b + b2
Giải câu hỏi Trang 10 SGK Toán 8 Tập 1
tính toán [a + (-b)]2 (trong đó a và b là các số tùy ý).
Hướng dẫn giải pháp
Áp dụng tổng bình phương bằng nhau, ta có:
[a + (-b)]2 = a2 + 2 * a * (-b) + (-b) 2 = a2 – 2 * a * b + b2Các câu hỏi SGK Toán lớp 8 Trang 11 Tập 1
ai đúng và ai sai?
a2 – 10a + 25 = (a – 5) 2
Tow viết:
a2 – 10 * a + 25 = (5 – a) 2.
Hương nhận xét: Thọ sai, Đức đúng.
Sơn nói: Với ví dụ trên, em có thể rút ra một phương trình rất đẹp!
Xin cho biết ý kiến của tôi. Sun có thể suy ra phương trình nào?
Hướng dẫn giải pháp
Cả Đức và Thọ đều đúng;
Nhận xét của Huang là sai;
Con đến phương trình: (a – 5) 2 = (5 – a) 2
Có thể bạn thích : Cú sốc U23 Nhật Bản bị loại từ vòng bảng
Giải bài 16 Trang 11 SGK Toán 8 Tập 1
Viết các biểu thức sau dưới dạng tổng hoặc chênh lệch bình phương:
a) a2 + 2a + 1
b) 9a2 + b2 + 6ab
c) 25a2 + 4b2 – 20ab
d) a2 – a + 1/4
Hướng dẫn giải pháp
a) Áp dụng hằng đẳng thức cho bình phương của tổng A = a và B = 1 (hằng đẳng thức)
a2 + 2a + 1
= a2 + 2a1 + (1) 2
= (a + 1) 2
b) Áp dụng hằng đẳng thức cho bình phương của tổng A = 3a và B = b (hằng đẳng thức)
9a2 + b2 + 6ab
= 9a2 + 6ab + b2
= (3a) 2 + 2.3ab + b2
= (3a + b) 2
c) Áp dụng hằng đẳng thức (hằng đẳng thức) để bình phương sự khác biệt của A = 5a và B = 2b
25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a) 2 – 2 * 5a * 2b + (2b) 2
= (5a – 2b) 2
d) Áp dụng hằng đẳng thức (hằng đẳng thức) A = hiệu bình phương của a và B = 1/2
a2 – a + 1/4
= a2 – 2 * a * 1/2 + (1/2) 2
= (a – 1/2) 2

Hi vọng các bạn đã hiểu được 7 Phương trình đáng nhớ (hằng đẳng thức) với bài chia sẻ vừa rồi của kubet. Đừng quên theo dõi kubet để không bỏ lỡ những kiến thức thú vị nhé.
Đăng ký KU casino | KUBET | tài khoản tổng

Tham gia nhiều trò chơi kiếm tiền cùng các mỹ nữ xinh đẹp chia bài, xóc đĩa , game xổ số
Trở lại Nhà cái KUBET đăng ký tham gia KU89 Trang tổng KU casino thuộc tập đoàn JZ.
